 +
+  +
+  +
+ 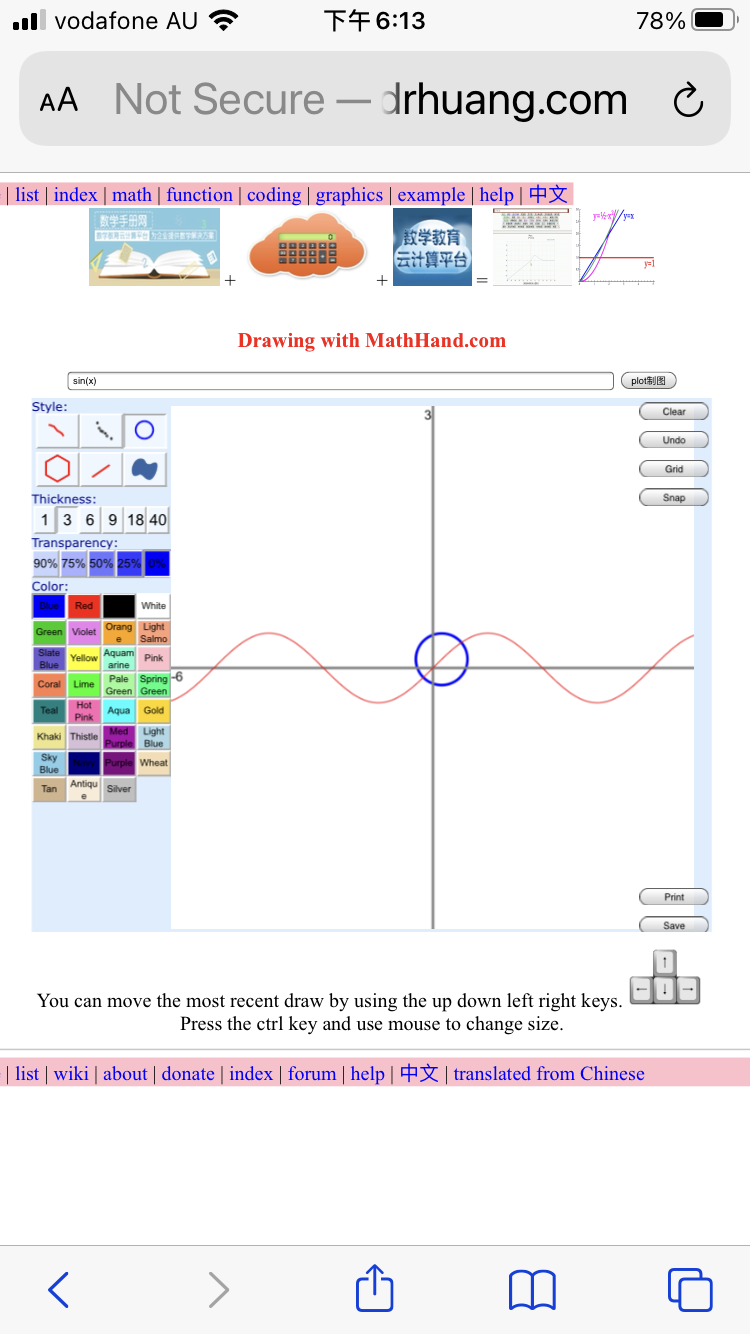 =
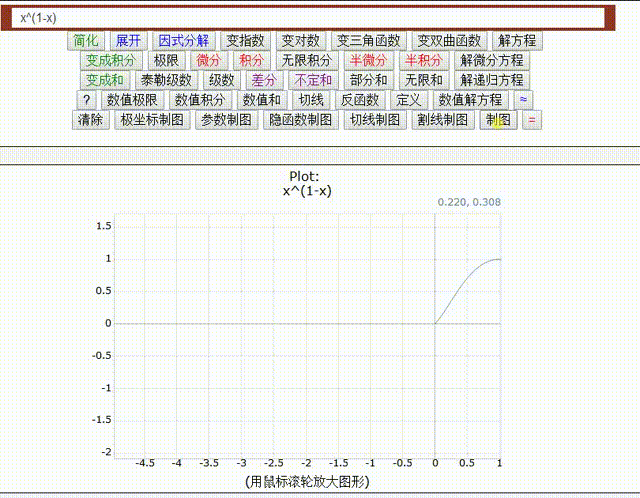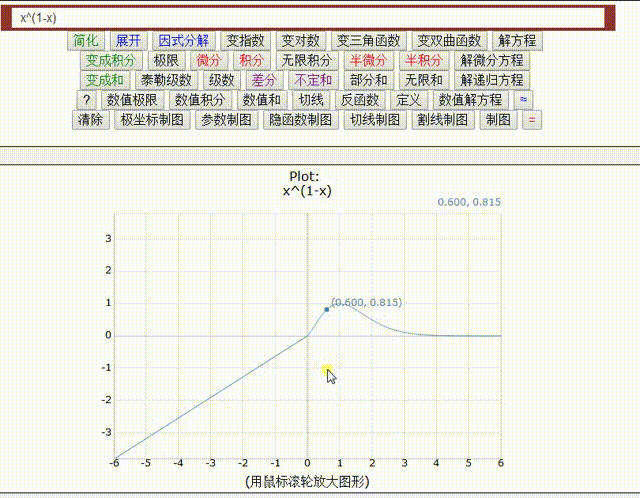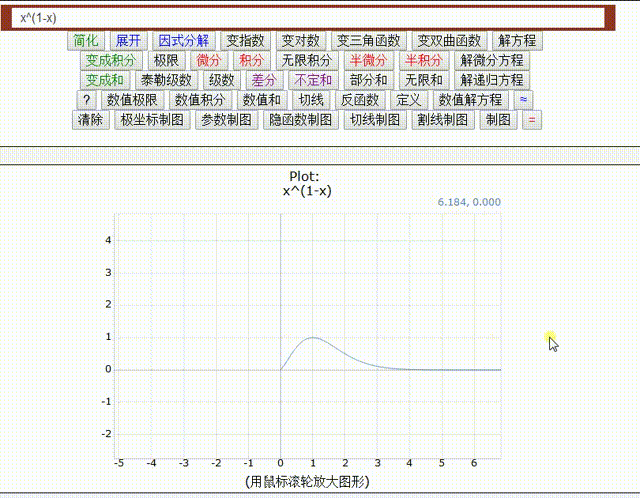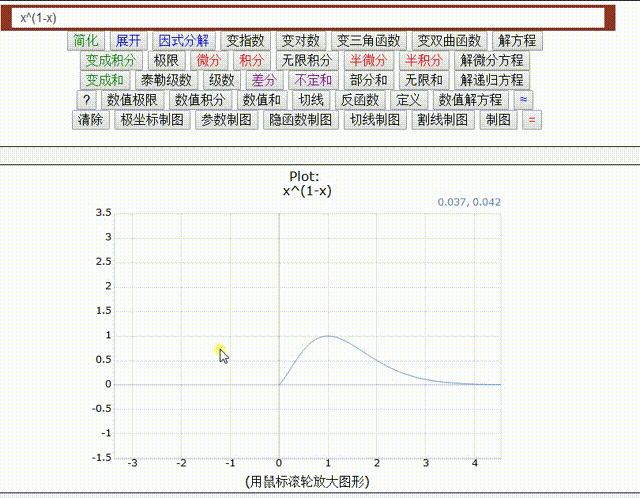
= 
 +
+  +
+  +
+  =
= 
直角三角形射影定理(又叫欧几里德(Euclid)定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。公式Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下: \[ \begin{array}{*{20}c} {1.} & {AD^2 = BD \cdot DC} \\ {2.} & {AB^2 = BD \cdot BC} \\ {3.} & {AC^2 = CD \cdot BC} \\ {4.} & {AB \cdot AC = BC \cdot AD} \\ \end{array} \]
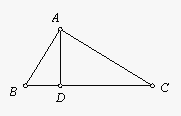
在△BAD与△BCD中,∵∠BDA=∠BDC=90°,且∠DBC+∠C=90°, ∴∠A=∠C,又∵∠BDA=∠BDC=90,∴△BAD∽△CBD,∴ AD/BD=BD/CD,即BD2=AD·DC.其余同理可得可证.
任意三角形射影定理又称“第一余弦定理”:△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有 \[ \begin{array}{l} a = b \cdot \cos C + c \cdot \cos B \\ b = c \cdot \cos A + a \cdot \cos C \\ c = a \cdot \cos B + b \cdot \cos A \\ \end{array} \] 由三角形的边角关系可以容易证明该定理
将任意三角形射影定理的三条公式作如下处理: \[ \left\{ \begin{array}{l} a^2 = ab \cdot \cos C + ac \cdot \cos B \\ b^2 = bc \cdot \cos A + ab \cdot \cos C \\ c^2 = ac \cdot \cos B + bc \cdot \cos A \\ \end{array} \right. \] 从上述三条等式中任取两条相加然后减去第三条等式: \[ \left\{ \begin{array}{l} a^2 + b^2 - c^2 = 2ab \cdot \cos C \\ b^2 + c^2 - a^2 = 2bc \cdot \cos A \\ c^2 + a^2 - b^2 = 2ac \cdot \cos B \\ \end{array} \right. \] 进一步处理,即可得到任意三角形余弦定理。
平面图形射影面积等于被射影图形的面积S乘以该图形所在平面与射影面所夹角的余弦。
cosθ=S射影/S原(平面多边形及其射影的面积分别是S原,S射影,它们所在平面所成锐二面角的为θ。)