 +
+  +
+  +
+  =
= 
 +
+  +
+  +
+  =
= 
在数学中,偏微分方程 (PDE) 是包含未知多变量函数及其偏导数的微分方程。 PDE 用于制定涉及多个变量的函数的问题, 要么由计算机解决,要么用于创建计算机模型。 一个特例是常微分方程 (ODE),它处理单变量及其导数的函数。
偏微分方程可用于描述各种现象,例如声音、热、扩散、静电学、电动力学、流体动力学、弹性、引力和量子力学。 这些看似不同的物理现象可以类似地用偏微分方程形式化。 正如常微分方程通常模拟一维动力系统一样,偏微分方程通常模拟多维系统。
分数阶微分方程(FDE)可以描述多个具有记忆的复杂非局部系统的动力学。 它们出现在许多科学和工程领域,如物理、化学、生物学、生物物理学、经济学、 控制理论、信号和图像处理等。特别是,描述不同现象的非线性系统可以用分数阶导数来建模。 在一些分数模型中也报道了混沌行为。 存在与分数阶微分方程初值和边值问题解的存在性和唯一性相关的理论结果[1-5]。
本文证明了分数阶微分方程的解析解是通过MathHand.com求解的。 MathHand.com是在线数学计算器,其前身是SymbMath [6-7]。 它被评论为数学手册计算器 [8]。 例子包括分数阶微分方程、分数阶偏微分方程、分数阶积分方程、分数阶微分和积分混合阶方程、 分数阶微分方程组、复阶微分方程组和变阶微分方程组。 默认情况下,此处使用分数阶微积分的 Caputo 定义 [9]。
表1. 不同阶次的比较
| 阶次 | 名称 | 方程 | y( ) | ds( ) | d( ) | ints( ) |
|---|---|---|---|---|---|---|
| 2 | 二阶 | `(d^2 y)/dx^2 - 2y = exp(x)` | y(2,x) | ds(y,x,2) | d(y(x),x,2) | |
| 1.5 | 1.5阶 | `d^1.5/dx^1.5 y - 2y = exp(x)` | y(1.5,x) | ds(y,x,1.5) | d(y(x),x,1.5) | |
| 1 | 一阶 | `dy/dx - 2y = exp(x)` | y(1,x) | ds(y ,x) | d(y(x),x) | |
| 0.5 | 半微分阶 | `d^0.5/dx^0.5 y - 2y = exp(x)` | y(0.5,x) | ds(y,x,0.5) | d(y(x),x,0.5) | |
| -0.5 | 半积分阶 | `d^-0.5/dx^-0.5 y - 2y = exp(x)` | y(-0.5 ,x) | ds(y,x,-0.5) | d(y(x),x,-0.5) | ints(y,x ,0.5) |
| -1 | 积分阶 | `int y\ dx-2y = exp(x)` | y(-1,x) | ds(y,x,-1) | d(y(x),x,-1) | ints(y,x) |
| -2 | 双积分阶 | `int int y\ (dx)^2 - 2y = exp(x)` | y(-2, x) | ds(y,x,-2) | d(y(x),x,-2) | ints(y,x, 2) |
| i | 复数阶 | `(d^i y)/dx^i - 2y = exp(x)` | y(i,x) | ds(y,x,i) | d(y(x),x,i) | |
| cos(x) | 变量阶 | `(d^cos(x) y)/dx^cos(x) - 2y = exp(x)` | y(cos(x),x) | ds(y,x,cos(x)) | d(y(x),x,cos( x)) |
将您的方程输入mathHand.com,单击“dsolve”按钮求解,然后单击“test”按钮测试其解。
例如
输入 y(1,x) - 2y = exp(x) 作为一阶微分方程
`y^((1))(x) - 2y = exp(x)`
或者输入 dsolve( ) 函数,单击“=”按钮求解,然后单击“test”按钮测试其解。
例如
输入 dsolve( ds(y) - 2y = exp(x) ) 对于
dsolve `dy/dx - 2y = exp(x)`
其解如表2所示。
表 2 不同阶次微分方程比较
| 阶次 | 名称 | 方程 | 一般解 | 特殊解 |
|---|---|---|---|---|
| 2 | 二阶微分方程 | `(d^2 y)/dx^2 - 2y = exp(x)` | `C_1*exp( sqrt(2)*x)` | -exp(x) |
| 1.5 | 1.5阶微分方程 | `d^1.5/dx^1.5 y - 2y = exp(x)` | `C_1*exp(2^ (2/3)*x)` | -exp(x) |
| 1 | 微分方程 | `d/dx y -2y = exp(x)` | `C_1*exp(2*x)` | -exp(x) |
| 0.5 | 半微分方程 | `d^0.5/dx^0.5 y - 2y = exp(x)` | `C_1*exp(4*x )` | -exp(x) |
| 0 | 0阶微分方程 | `d^0/dx^0 y - 2y = exp(x)` | 0 | -exp(x) |
| -0.5 | 半积分方程 | `d^-0.5/dx^-0.5 y - 2y = exp(x)` | `C_1*exp (1/4*x)` | -exp(x) |
| -1 | 积分方程 | `int y\ dx-2y = exp(x)` | `C_1*exp(1/2*x) ` | -exp(x) |
| -2 | 二重积分方程 | `int int y\ (dx)^2 - 2y = exp(x)` | `C_1*exp( 1/sqrt(2)*x)` | -exp(x) |
| i | 复阶微分方程 | `d^i/dx^i y - 2y = exp(x)` | `C_1*exp(1/2 ^i*x)` | -exp(x) |
| cos(x) | 变阶方程 | `(d^cos(x)y)/dx^cos(x) - 2y = exp(x)` | `C_1*E_cos(x)(2x^cos(x))` | -exp(x) |
上表表明,无论其阶数如何,它们的微分方程的特解都是相同的。
泊松方程
Δy = ρ
其中ρ是已知函数,Δ是拉普拉斯算子。
例如 圆狄利克雷问题解的泊松积分。
`r^2*(d^2y)/(dr^2)+r*dy/(dr) = 1`
研究形式的波动方程
`(d^2y)/dt^2-a^2 Δ y = f(t,x,v,z)`
其中 f( x , v , z , t ) 是已知函数。
齐次方程柯西问题的解
例如 一维波动方程:
`(d^2y)/dt^2 - a^2 * (d^2y)/dx^2 =0 `
例如 二维波动方程。 二维拉普拉斯方程的连续解称为调和函数
`(d^2y)/(dt^2) - a^2 * ((d^2y)/dx^2 + (d^2y)/(dz^2)) = 0`
例如 三维波动方程:
`(d^2y)/(dt^2) - a^2 * ((d^2y)/dx^2 + (d^2y)/(dv^2) + (d^2y)/(dz^2))=0 `
其解如表2所示。积分方程两边同时求微分即可转化为微分方程,然后求解。
通过 dsolve( ) 求解 y 的(分数)微分方程,例如
dsolve( `d^0.5/dx^0.5 y = 2y` )
其解如表 2 所示。分数阶微分方程的性质与微分方程相同:
线性分数阶微分方程的解 = 通解 + 特殊解 = gsolution( ) + psolution( )
它与线性微分方程类似,因此分数阶微分方程的求解方法与微分方程类似[3-5]。
例如 具有分数时间阶次的一维扩散方程:
`(d^0.5y)/dt^0.5 - a^2* (d^2y)/dx^2 =0`
在方程左侧输入 ds(y,t,0.5)=ds(y,x,2)-ds(y,x)-exp(x)-exp(t) 作为半偏微分时间 t, 例如 当a=1时,f(t,x)=exp(t)+exp(x),方程变为
`(d^0.5y)/dt^0.5 = (d^2y)/dx^2-exp(x)-exp(t)`
例如 具有分数时间阶次的二维扩散方程:
`(d^0.5y)/dt^0.5 = (d^2y)/dx^2+(d^2y)/(dz^2)-exp(x)`
其解如表 2 所示。默认情况下,dsolve( ) 使用分数阶微积分的 Caputo 定义。 如果您想使用黎曼定义,请使用拉普拉斯变换求解器lasolve( )。 Caputo 定义和 Riemann-Liouville (R-L) 定义之间的差异参见分数阶微积分的第 6 节 [8]。 例如
dsolve(y(-0.5,x)=1) 给出零 。
lasolve(y(-0.5,x)=1) 给出非零值 。
通过两边同时求微分,可以将积分方程转化为微分方程。 同理,分数阶积分方程也可写为 转化为分数阶微分方程,然后求解。
将微分方程组按分数阶推广为分数阶微分方程组。 例如
`( d^0.5x)/dt^0.5 = 2x, (d^0.5y)/dt^0.5 = x+y`
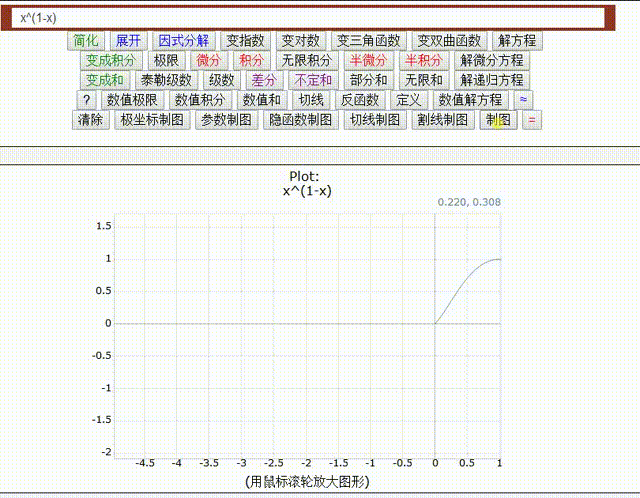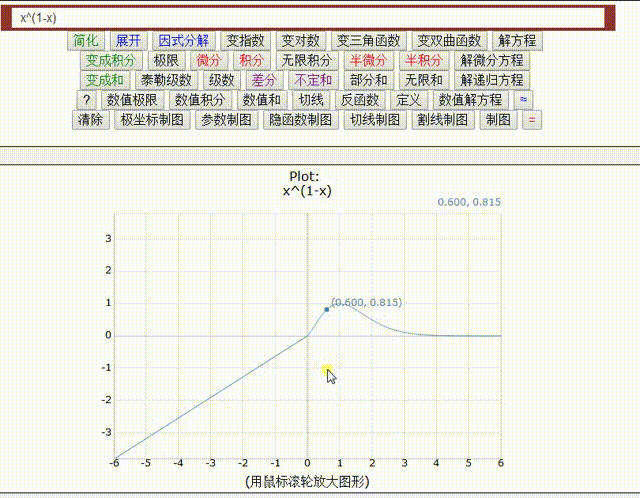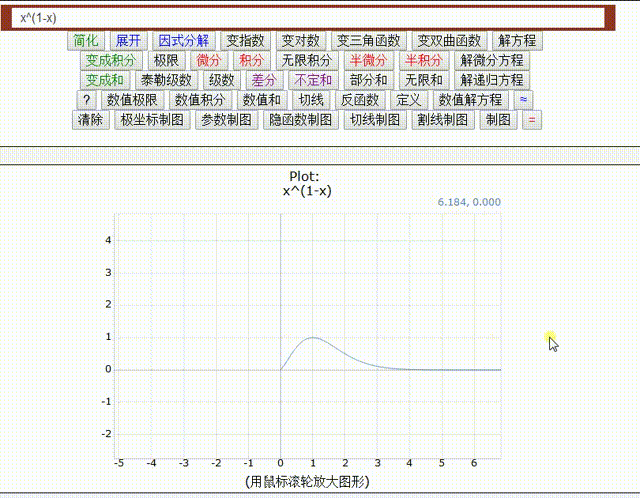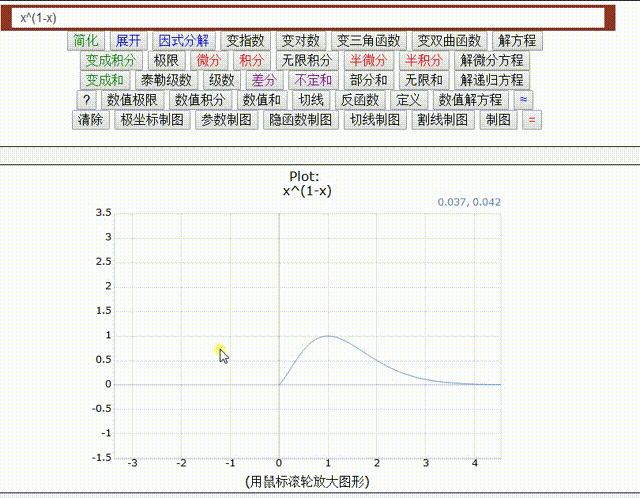
阶数的变化类似于下面动画图1中n阶分数导数`d^n/dx^n x`的变化。
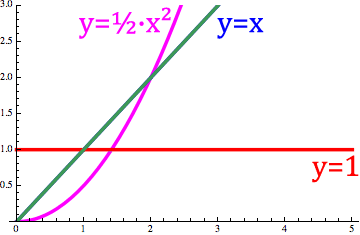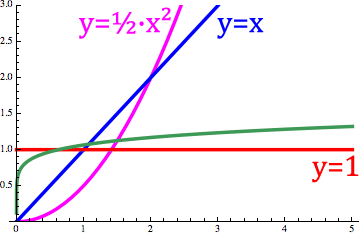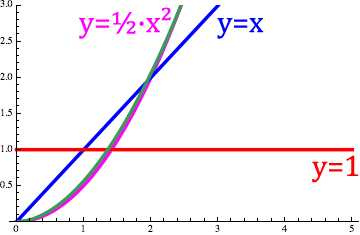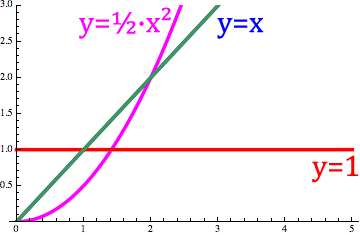
图 1. 阶次在 1 和 -1 之间变化的动画。
我们希望本文中概述的示例和想法对 微分方程的初级和高级课程,以及 解决实践中研究和设计问题中出现的微分方程。