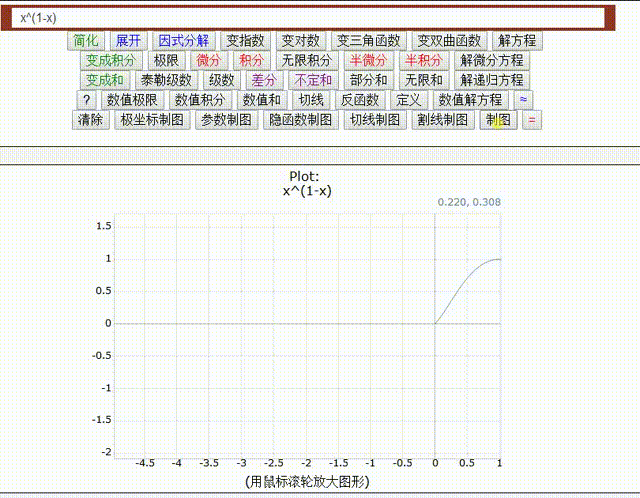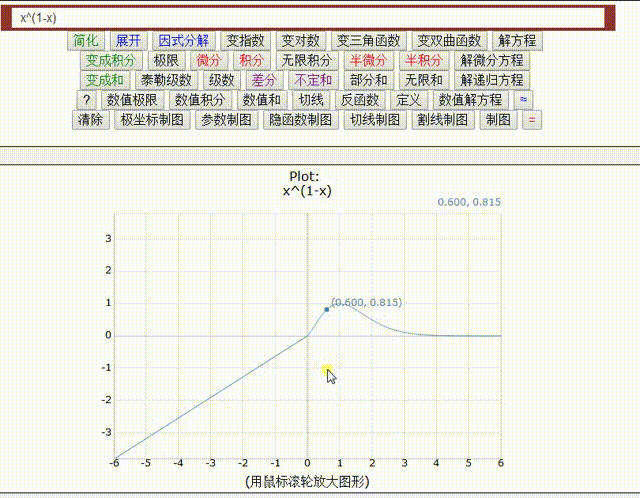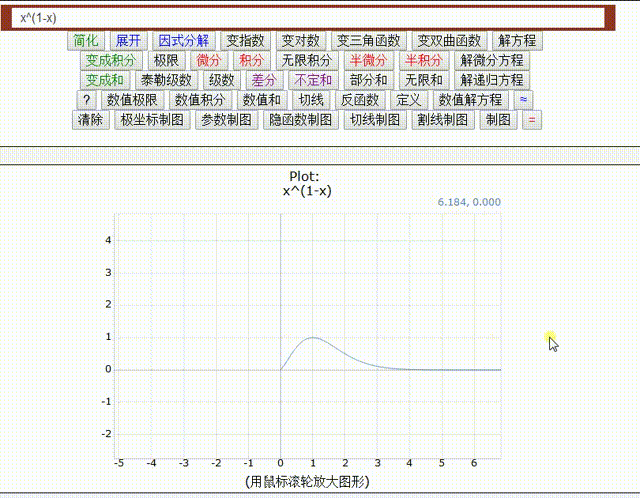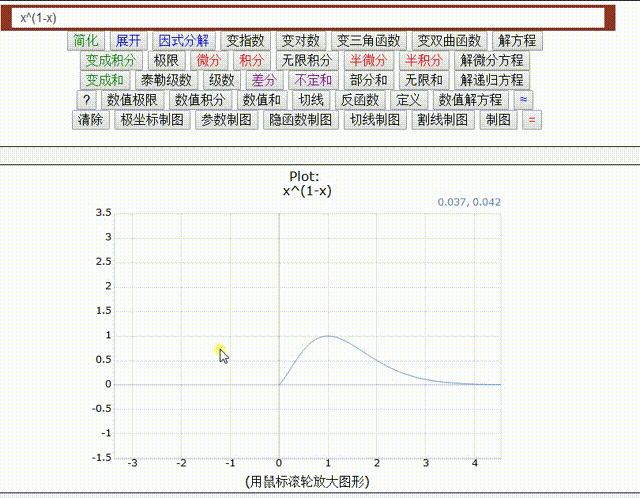
黄博士网: 教育网, AI数学手册计算器软件，电化学虚拟实验室，虚拟电化学工作站，电化学软件 首页 | 目录 | 世界 | 学科 | 文科 | 科学 | 数学 | 物理 | 化学 | 医学 | 计算 | 软件 | 帮助 | 打赏
+ + + =

双伽玛函数 digamma(x)

双伽玛函数 是伽玛函数的对数 loggamma(x) 的导数，通常用 ψ0(x)、ψ0(x) 或 digamma(x) 来表示。

\[ \psi(x) = \frac{d}{dx} \ln{\Gamma(x)} = \frac{\Gamma'(x)}{\Gamma(x)} \]

它是第一个多伽玛函数 polygamma(x) = polygamma(0,x) 。

目录

与调和数的关系

双伽玛函数与调和数有以下的关系：

\psi(n) = H_{n-1}-\gamma\!

其中Hn是第n个调和数，γ是欧拉-马歇罗尼常数。对于半整数的值，它可以表示为：

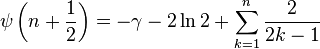
\psi\left(n+{\frac{1}{2}}\right) = -\gamma - 2\ln 2 + \sum_{k=1}^n \frac{2}{2k-1}

积分表示法

它有以下的积分表示法：

\psi(x) = \int_0^{\infty}\left(\frac{e^{-t}}{t} - \frac{e^{-xt}}{1 - e^{-t}}\right)\,dt

也可以写为

\psi(s+1)= -\gamma + \int_0^1 \frac {1-x^s}{1-x} dx

这可以从调和数的欧拉积分公式得出。

泰勒级数

双伽玛函数有一个有理ζ级数，由z=1的泰勒级数给出。这是

\psi(z+1)= -\gamma -\sum_{k=1}^\infty \zeta (k+1)\;(-z)^k,

当|z|<1时收敛。在这里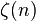，\zeta(n)是黎曼ζ函数。这个级数可以很容易从赫尔维茨ζ函数的泰勒级数推导出。

牛顿级数

双伽玛函数的牛顿级数可从欧拉积分公式得出：

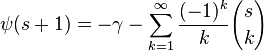
\psi(s+1)=-\gamma-\sum_{k=1}^\infty \frac{(-1)^k}{k} {s \choose k}

其中\textstyle{s \choose k}是二项式系数。

反射公式

双伽玛函数满足一个反射公式，类似于伽玛函数的反射公式：

\psi(1 - x) - \psi(x) = \pi\,\!\cot{ \left ( \pi x \right ) }

递推关系

双伽玛函数满足以下的递推关系：

\psi(x + 1) = \psi(x) + \frac{1}{x}

高斯和

双伽玛函数具有以下形式的高斯和：

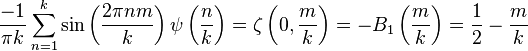
\frac{-1}{\pi k} \sum_{n=1}^k \sin \left( \frac{2\pi nm}{k}\right) \psi \left(\frac{n}{k}\right) = \zeta\left(0,\frac{m}{k}\right) = -B_1 \left(\frac{m}{k}\right) = \frac{1}{2} - \frac{m}{k}

其中m是整数，且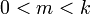0<m<k。在这里，ζ(s,q)是赫尔维茨ζ函数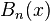，B_n(x)是一个伯努利多项式。乘法定理的一种特殊情况是：

\sum_{n=1}^k \psi \left(\frac{n}{k}\right) =-k(\gamma+\log k),

一个推广为：

\sum_{p=0}^{q-1}\psi(a+\frac{p}{q})=q[\psi(qa)-\ln(q)],

其中假设了q是自然数，而1-qa则不是。

高斯双伽玛定理

对于正整数 m \,和 k \, \left(m<k \right)\,，双伽玛函数可以用初等函数来表示：

\psi\left(\frac{m}{k}\right) = -\gamma -\ln(2k) -\frac{\pi}{2}\cot\left(\frac{m\pi}{k}\right) +2\sum_{n=1}^{\lfloor \frac{k-1}{2}\rfloor} \cos\left(\frac{2\pi nm}{k} \right) \ln \sin\left(\frac{n\pi}{k} \right)

特殊值

双伽玛函数有以下的特殊值：

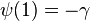
\psi(1) = -\gamma\,\!
\psi\left(\frac{1}{2}\right) = -2\ln{2} - \gamma
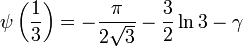
\psi\left(\frac{1}{3}\right) = -\frac{\pi}{2\sqrt{3}} -\frac{3}{2}\ln{3} - \gamma
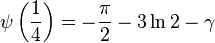
\psi\left(\frac{1}{4}\right) = -\frac{\pi}{2} - 3\ln2 - \gamma
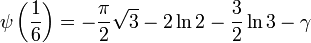
\psi\left(\frac{1}{6}\right) = -\frac{\pi}{2}\sqrt{3} -2\ln{2} -\frac{3}{2}\ln3 - \gamma
\psi\left(\frac{1}{8}\right) = -\frac{\pi}{2} - 4\ln{2} - \frac{\sqrt2}{2} \left[\pi + \ln(3+2\sqrt{2})\right] - \gamma
\psi\left(\frac{3}{4}\right) = \frac{\pi}{2} - 3\ln{2} - \gamma

参见

Reference

  • gamma
  • special function